Repeating Decimals

Awhile back as a class we investigated repeating decimals. After some work and discussion, we came to see that when doing the long division of the fraction, if you arrive at the same remainder twice then you have a repeating decimal. For example consider 1/6:

Each reminder will keep being a multiple of 4, which 6 will continue to go into by the same amount each time. Pretty cool.

Then we all went home with the task of investigating repeating decimals further on our own.

What immediately came to my mind to look into was if there were a way to look at the fraction and tell if it would be repeating decimal without doing the long division or typing it into your calculator. My first thought was just that maybe it dealt with the denominator being prime, since I had been focusing on a 1/3 for some time. But this was quickly, like the second after thought, proven wrong. There's a 1/5 and a 1/2, and 1/6 repeats but 6 is not prime. Then I realized I should probably come up with a couple more examples of repeating decimals, so know what the numbers look like. Here's the list I got: 1/3, 1/6, 1/7, 1/9, 1/11, 1/12, 1/13, 1/14, 1/15, 1/17, 1/18.

I also knew that certain multiples of these would become non-repeating (so I would have to look at fractions in simplified form). I noticed from my list that 1/6, 1/9, 1/12, 1/15, and 1/18 related to a 1/3 since multiples of them could be reduced to a third. They are also was of breaking down a 1/3 into smaller pieces, so it makes sense that they would be repeating decimals as well. I then looked at 1/7 and thought to myself that anything with a denominator a multiple of 7 will be a repeating decimal. I then checked: 1/14, 1/21, 1/28. What do you know, it worked. So it would likewise follow for 11, 13, 17, and 19 (the denominators of other repeating decimals I recorded).

I then noticed something all these numbers had in common, their denominators were composed of more than just 5 and 2 (the prime factors of 10). Those composed of only 5 and 2 or that could be simplified to such were not repeating: 1/5, 1/2, 1/4, 1/8, 1/10, 1/20.

I was curious as to why and might explore that later. I had a thought that since the numbers the denominator is compose of go into 10, when doing the long division you would eventually have a point when that value goes into the reminder (a multiple of 10) completely. But I was content with my findings and had fun processing through it: asking different questions, gathering more examples, analyzing what I had, and then being able to make a conclusion and reach an understanding on what I had set out on,

Understanding Division by Fractions

After reading an article by Richard R. Skemp discussing relational vs. instrumental understanding, in class we discussed how we had learned fraction operations (addition, subtraction, multiplication, division). For me and the people in my group, most of us had learned through instrumental understanding. We were taught a rule to memorize and apply in the given situation in order to solve the problem. A "rules without reasons" way of learning.

As we went over the different operations, for all of the first 3, addition, subtraction, and multiplication, we felt we had a good understanding of them. The answers we would get from problems made sense to us and we could explain to someone verbally why. However, when it came to division with fractions, we were a little stumped. Most of us were taught the rule of flipping the denominator and numerator of the fraction you are dividing by and then multiplying that with the other fraction. We knew the rule well and could explain to someone how to solve it. But why was the answer the way it was?

 I thought this was sort of interesting. Why was it so difficult?

I think part of the difficulty comes from the fact that we often don't talk about dividing by fractions. Another part might be that we did not have a good idea of how to visualize what was happening or to describe the process. After looking into division with fractions, these two things coming together really helped.

1). Verbally:
Knowing how to read a division by fractions problem is really important. This helps you to understand what you are solving for. For example, given: 1\2 ÷ 1/4, what is being asked is how many fourths are in a half. This relates right back to division with integers, like 6 ÷ 3 is asking how many 3's are in 6. Once we see that this is what is being asked, we can better represent it with a picture and also understand our answer.

2) Pictorially:
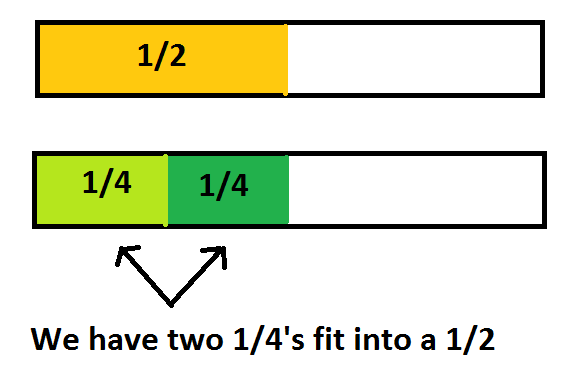
Keeping with the same problem (1\2 ÷ 1/4), it's helpful to begin with drawing what a whole is. After this, we can mark in what a half is and what a fourth of our whole will look like.Then it simply becomes finding out how many fourths will fit into the half.

We see that two will fit, so our answer is two.

3) Making sense of it all:
We can reason to see that the answer we got is correct. Remember, we're finding how many groups of a 1/4 go into a 1/2. We already know that a 1/4 is less than a 1/2, so we should expect our answer to be at least greater than one. Thinking in the same way, we can reason through other division by fraction problems. Like 4 ÷ 5/6 for example. We know that 5/6 is less than one whole, so we should expect our answer to be at least greater than one. We also know that we have four whole pieces, so we should expect for each whole that at least more than one 5/6 will fit into it, so our answer should be at least more than 4.
What if the dividend is smaller than the divisor? Let's look at the example of 1\3 ÷ 1/2. Since 1/2 is larger than 1/3 we should expect our answer to be less than 1, since not even one 1/2 will fit into the 1/3.


Having a better understanding of what fraction division problems are saying allowed me to think through the problem and reason where the answer should be, as well as to better understand how to visualize and model what is happening. Building a relational understanding of fraction division really helps to better understand it and now for me to help explain to others how to do it and incorporate the use of models effectively.